Answer:
3xy
Explanation:
We are to determine the GCF of the expression.
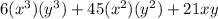
THe GCF of the expression is the term that exactly divides all the terms in the expression
Step 1
If we observe the expression carefully, we notice that it has a common term of 3, x and y. That is, 3,x and y divides each term.
Step 2
Divide by 3xy for confirmation
![3xy\left((6(x^3)(y^3))/(3xy) +(45(x^2)(y^2))/(3xy)+(21xy)/(3xy)\right)\\=3xy[2(x^2)(y^2)+15xy+7]](https://img.qammunity.org/2021/formulas/mathematics/college/amvl13lh7qv0r76709kmhwywse002k310v.png)
Therefore, we can confirm that the GCF is 3xy.