Question

Determine the eccentricity, the type of conic, and the directrix for r =2.1/1+0.7cod theta​

Answer 1

c

Explanation:

c

Answer 2

The equation represents an ellipse with an eccentricity of 0.7.

Explanation:

The given equation is

`r=(2.1)/(1+0.7cos\theta)`

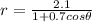
This equations represents a conic section in polar form, where the coefficient of the cosine function is the eccentricity of the conic section.

So, in this case, the eccentricity is
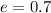`e=0.7`, which indicates that the equation belong to an ellipse, because the eccentricy of ellipses are between 0 and 1.

Therefore, the equation represents an ellipse with an eccentricity of 0.7.