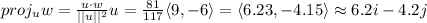Answer:
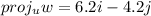
Explanation:
The projection of a vector
 onto a vector
onto a vector
 is defined as the projection of the vector
is defined as the projection of the vector
 on the line that contains the vector
on the line that contains the vector
 . It can be calculated using the following formula:
. It can be calculated using the following formula:
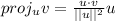
Where:

Is the dot product between
 and
and
 which is given by:
which is given by:
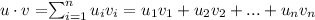
and:
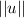
Is the magnitude of vector which can be calculated as follows:
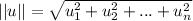
In this sense, the projection of vector w onto vector u is:
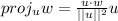
Where the dot product between
 and
and
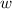 is:
is:
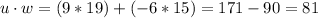
And the magnitude of
 is:
is:
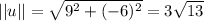
Thus: