Please consider the attached file.
We can see that triangle JKM is a right triangle, with right angle at M. Segment KM is 6 units and segment MJ is 3 units. We can also see that KJ is hypotenuse of right triangle.
We will use Pythagoras theorem to solve for KJ as:

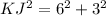
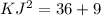
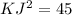
Now we will take positive square root on both sides:
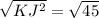
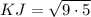
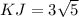
Therefore, the length of line segment KJ is
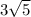 and option D is the correct choice.
and option D is the correct choice.