Question

Dos cargas q_1=-8μC y q_2=13μC se encuentran a una distancia r=0.12 m. ¿Cuál es la fuerza resultante sobre una tercera carga q_3=-4μC, situada en el centro de la distancia que separa las cargas q_1 y q_2?

Answer 1

209.53 N

Step-by-step explanation:

To find the force on the third charge you use the Coulomb formula:

`F=k(q_1q_2)/(r^2)`

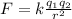
k: Coulomb's constant = 8.98*10^9 Nm^2/C^2

The force on the third charge is the contribution of the force between the third charge and the other ones:

`F=F_1+F_2`

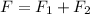
By taking into account that the third charge is at the middle of the distance between charge 1 and charge 2 you have r = 0.12m/2 = 0.06m

Furthermore, you take into account that the first charge repels the third charge and the second charge attracts the third charge.

By replacing you have:

`F=k(q_1q_3)/(r^2)+k(q_2q_3)/(r^2)\\\\F=(k)/(r^2)q_3[q_1+q_2]\\\\F=((8.98*10^9Nm^2/C^2)(4*10^(-6)C))/((0.06m)^2)[8*10^(-6)C+13*10^(-6)C]\\\\F=209.53\ N`

Hence, the force between on the third charge is 209.53 N