Answer:
Explanation:
some rules of logarithmic function
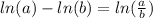
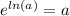
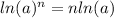 vice-versa
vice-versa
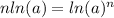
If ㏑(a) = ㏑(b), then a = b
∴

Use the 2nd rule to simplify it
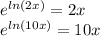
2㏑(2x) - ㏑(10x) = ㏑(30)
Use the 3rd rule in the 1st term
∵ 2㏑(2x) = ㏑(2x)² = ㏑(4x²)
∴ ㏑(4x²) - ㏑(10x) = ㏑(30)
- Use the 1st rule with the left hand side

Use the 4th rule
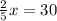
Multiply both sides by 5
∴ 2 x = 150
- Divide both sides by 2
∴ x = 75
The value of x = 75