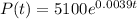Question

In 2013, the moose population in a park was measured to be 5,100. By 2018, the population was measured again to be 5,200. If the population continues to change exponentially, find an equation for moose population, P, as a function of t, the years since 2013

Answer 1

`P(t) = 5100e^(0.0039t)`

Explanation:

The exponential model for the population in t years after 2013 is given by:

`P(t) = P(0)e^(rt)`

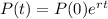
In which P(0) is the population in 2013 and r is the growth rate.

In 2013, the moose population in a park was measured to be 5,100

This means that
`P(0) = 5100`

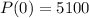
So

`P(t) = 5100e^(rt)`

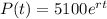
By 2018, the population was measured again to be 5,200.

2018 is 2018-2013 = 5 years after 2013.

So this means that
`P(5) = 5200`.

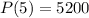We use this to find r.

`P(t) = 5100e^(rt)`

`5200 = 5100e^(5r)`

`e^(5r) = (52)/(51)`

`\ln{e^(5r)} = \ln{(52)/(51)}`

`5r = \ln{(52)/(51)}`

`r = \frac{\ln{(52)/(51)}}{5}`

`r = 0.0039`

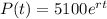
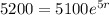
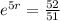
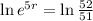
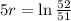
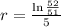
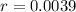
So the equation for the moose population is:

`P(t) = 5100e^(0.0039t)`