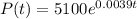Answer:
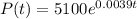
Explanation:
The exponential model for the population in t years after 2013 is given by:

In which P(0) is the population in 2013 and r is the growth rate.
In 2013, the moose population in a park was measured to be 5,100
This means that

So
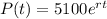
By 2018, the population was measured again to be 5,200.
2018 is 2018-2013 = 5 years after 2013.
So this means that
 .
.
We use this to find r.
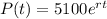
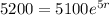
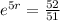

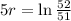
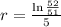
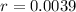
So the equation for the moose population is: