Question

7.4 A pretimed four-timing-stage signal has critical lane group flow rates for the first three timing stages of 200, 187, and 210 veh/h (saturation flow rates are 1800 veh/h/ln for all timing stages). The lost time is known to be 4 seconds for each timing stage. If the cycle length is 60 seconds, what is the estimated effective green time of the fourth timing stage?

Answer 1

16 seconds

Step-by-step explanation:

Given:

C = 60

L = 4 seconds each = 4*4 =16

In this problem, the first 3 timing stages are given as:

200, 187, and 210 veh/h.

We are to find the estimated effective green time of the fourth timing stage. The formula for the estimated effective green time is:

`g = ((v)/(s)) ((C)/(X))`

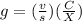
Let's first find the fourth stage critical lane group ratio
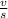`(v)/(s)` , using the formula:

`C = (1.5L +5)/(1 - ( (200)/(1800) + (187)/(1800) + (210)/(1800)) + ( (v)/(s)))`

`60 = (1.5*16 + 5)/(1 - ( (200)/(1800) + (187)/(1800) + (210)/(1800)) + ( (v)/(s)))`

`60 = (24+5)/(1 - (0.332 + ( (v)/(s))))`

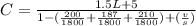
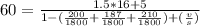
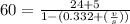
Solving for
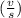`((v)/(s))`, we have:

`((v)/(s)) = 0.185`

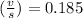
Let's also calculate the volume capacity ratio X,

`X = ((200)/(1800) + (187)/(1800) + (210)/(1800) + 0.185)((60)/(60-16)`

X = 0.704

For the the estimated effective green time of the fourth timing stage, we have:

`g_4 = ((v)/(s)) ((C)/(X))`

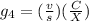
Substituting figures in the equation, we now have:

`g_4 = (0.185) ((60)/(0.704))`

`g_4 = 15.78 seconds`

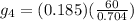
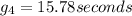
15.78 ≈ 16 seconds

The estimated effective green time of the fourth timing stage is 16 seconds