Answer:
The number of plates that can be made without repetition is 3124550.
Explanation:
The appropriate way to determine the number of plates to be made is by the application of combination.
Since the digits has 9 elements and the letters have 26, then 26
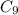 .
.
So that:
n
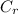 =
=
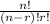
n = 26 and r = 9;
26
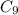 =
=
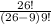
=
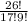
=
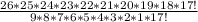
=
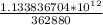
= 3124550
The number of plates that can be made without repeating numbers and letters is 3124550.