Answer:
The area of the sector to nearest hundredth is 35.33
Explanation:
Formula for calculating the area of a sector is given as
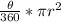 where;
where;
r is the radius of the circle
theta is the angle substended by the sector.
Given r = 5 and central angle theta =

Area of the sector is expressed as shown;
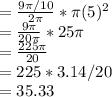
The area of the sector to nearest hundredth is 35.33