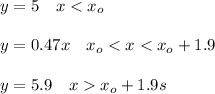Question

A drone is monitoring the atmospheric conditions above a farm field.

The drone hovers 5 meters above the crop line. Suddenly, it rises to approximately 5.9 meters (which takes 1.9 seconds)

to avoid colliding with the sprinkler system. Based on this information, which equations could model the height, y, of the

drone as a function of time, x?

Answer 1

`y=5 \ \ \ x<x_o\\\\y=0.47x\ \ \ x_o < x < x_o+1.9\\\\y=5.9\ \ \ x > x_o + 1.9s`

Explanation:

This situation can be considered as a piecewise function. First, you take xo as the time in which the drone goes upward. Before this time the height of the drone is constant with a value of 5 m. Next, you take into account that during 1.9 s after xo the drone accelerates. Finally, the drone flies again with a constant height of 5.9m. Hence, this function has three parts:

For the first part you have:

y = 5 for x < xo

For the second part you first calculate vertical speed (which means the slope of the linear function) by using the following kinematic equation:

`y=vx\\\\v=(y-y_o)/(x)=(5.9m-5.0m)/(1.9s)=0.47m/s`

Then you have:

y = 0.47x for xo < x < xo + 1.9s

And for the third part:

y = 5.9 for x > xo + 1.9s

Summarizing you obtain:

`y=5 \ \ \ x<x_o\\\\y=0.47x\ \ \ x_o < x < x_o+1.9\\\\y=5.9\ \ \ x > x_o + 1.9s`