Answer:
(a) h(t) = 3
(b) time = 1.36 seconds
Step-by-step explanation:
equation: h(t) = -16(t)² + 24t
Part A
If the fielder catches the ball at the height of about 3 ft.
Part B
using graphing technology, graphed below. (height, y = 3)
Additional *solving part B algebraically*
-16(t)² + 24t = 3
-16(t)² + 24t - 3 = 0
using quadratic equation
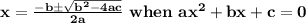
==================================
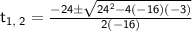
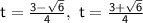
t = 1.36 seconds and 0.14 seconds
The fielder shall catch the ball when the ball is falling, so time : 1.36 s