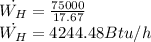Answer:
Step-by-step explanation:
Temperature of the house,
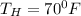
Convert to rankine,
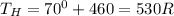
Heat is extracted at 40°F i.e

Calculate the coefficient of performance of the heat pump, COP
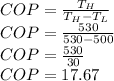
The minimum power required to run the heat pump is given by the formula:
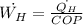 ...............(*)
...............(*)
Where the heat losses from the house,
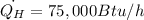
Substituting these values into * above