Question

There are 8 baseball players in the dugout for practice. Each player shakes hands with each of the other player ONLY ONCE.

How many handshakes are there?

Answer 1

8 players in total

Step-by-step explanation:

Answer 2

Answer: 28

Step-by-step explanation:

There are 8 players. For each player, there are 7 people to shake hands with. So we have 8*7 = 56 handshakes so far; however, we double count since the sequence AB is the same as BA (where A and B are player names). Order does not matter when it comes to shaking hands. So we have to divide by 2 to fix the double count. We go from 56 to 56/2 = 28. There are 28 different combinations.

You can use the formula
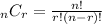`_nC_r = (n!)/(r!(n-r)!)` with n = 8 and r = 2, but the formula is a bit confusing to be honest if you aren't familiar with it. The exclamation marks indicate factorials.

Extra info: The value 28 can be found in Pascals triangle. Look at the row that starts with 1, 8, ... then note how 28 is in the third slot. Keep in mind that you start at r = 0 and count up by 1. So r = 2 corresponds to the third slot.