Answer:
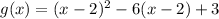
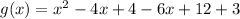
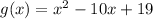
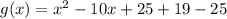
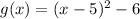
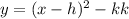
Where h,k represent the vertex and we got:
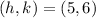
(5,6)
Explanation:
We have this original function given :

And we want to find the vertex for this new function
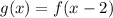 and we have:
and we have:
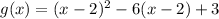
And solving the square we got:
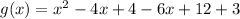
And adding similar terms we got:
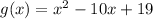
Now we can complete the square like this:
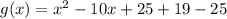
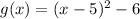
The general equation is given by:
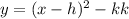
Where h,k represent the vertex and we got:
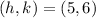
(5,6)