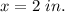Answer:2 in.
Explanation:
Given
Dimension of photo frame is

If the photo cover an area of
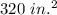
Suppose x be the width of border
Therefore dimension of frame without border is
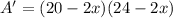
And
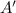 must be equal to
must be equal to
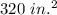
So,
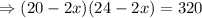
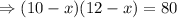
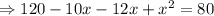
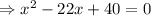

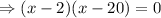
Thus there are two values of x out of which
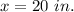 is not valid because it is not feasible
is not valid because it is not feasible
thus width of border is