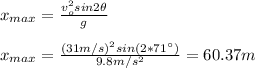Answer:
vx = 10.09 m/s
vy = 29.31 m/s
t = 5.98 s
ymax = 43.83 m
xmax = 60.37 m
Step-by-step explanation:
A) The horizontal speed is constant in the complete trajectory. It is given by:
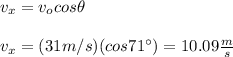
B) The vertical initial speed is:
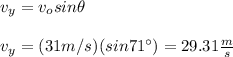
C) The flight time is given by:
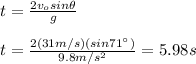
D) The maximum height is:
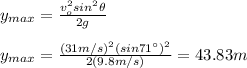
E) The maximum horizontal distance is: