Answer:
Eroor: LM² = 23² - 20² - 2(23)(20) cos 119°
Should be LM² = 23² + 20² - 2(23)(20) cos 119°
Lm² = 575.02 is incorrect
LM² = 1375.016 is correct
LM = 24.0 is incorrect
LM = 37 - 1 is correct
Answer: LM = 37 - 1
Explanation:
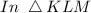
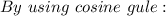
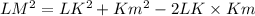
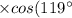
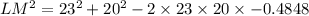
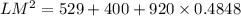
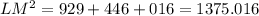
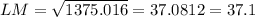
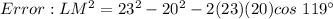
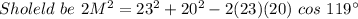
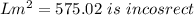
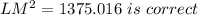
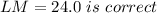
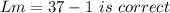
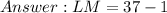
I hope this helps you
:)