Question

2. Jeff is trying to "get with" Slater. Being a calculating player, Jeff knows that his population proportion of landing a date is 69 percent. Jeff is going to make advances on Slater until success, so let us model the situation with a geometric distribution.2 (a) What is the probability that Jeff needs exactly 3 advances? (b) What is the probability that Jeff needs at least 3 advances? (c) Given that Jeff already made 4 advances, what is the probability that Jeff will need at least 3 more advances? (d) Show that all of the possibilities do indeed add up to 100 percent.

Answer 1

A) 0.0066309 ; B) 0.0961 ; D) Proven

Explanation:

Geometric Distribution : X ~
`q^(x-1) . p`

p = 0.69 ; q = 1- p = 1 - 0.69 = 0.31

A) P (x = 3) =
`(0.31)^(3-1) (0.69) = 0.31^2 (0.69) = 0.0961(0.69)= 0.0066309`

B) P (x > 3) = 1 - [ P(x =1) + P(x = 2) ]

`1 - [(0.31)^0 (0.69) + (0.31)^1(0.69)] = 1 - (0.69 + 0.2139) = 1 - 0.9039 = 0.0961`

D) P (x > 1) = P (x =1) + P (x = 2) + P (x = 3) ...............

= p + pq + pq^2 + pq^3 ........ [Geometric series with a = p , r = q]

Sum of infinite geometric series = a / (1- r)

p / (1-q) = 0.69 / (1-0.31) = 0.69 / 0.69 = 1 {Hence Proven}

Answer 2

`\bf a) - 0.0663\\b) - 0.31\\c) - 0.021\\d) - 1 or 100%`

Explanation:

`Let\;p = 69\;\% =0.69`

`So, p(x)=q^(x-1)p`
`-(i)`

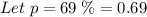
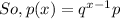
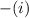
a) - The probability which Jeff requires at exactly three advances that is,

Then, put the value of
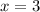`x=3` in eq - i

`p(x=3)=(0.31)^(3-1)(0.69)`

`p(x=3)=0.0663`

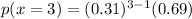
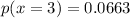
b) - The probability which Jeff requires at least three advances that is,

`p(x\geq1)=1-p`

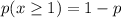
Put the value of
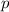`p` in the eq

`p(x\geq 2)=1-0.69=0.31`

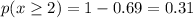
c) - Considering that he has only made four advances, the probability would be that he will require at least three more advances that is.

`p((x=7)/(x\geq 4)) = (p(x=7\;\cap\;x\geq 4))/(p(x\geq 4))`

`p((x=7)/(x\geq 4)) = (p(x=7))/(1-p(x\leq 3))`

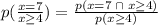
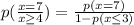
Then, put the value in the eq - i

`=((0.31)^(7-1)(0.69))/(1-\sum_(x=1)^(3)(0.31)^(x-1)(0.69))`

`=(0.0006)/(1-0.9702)`
`=0.0201`

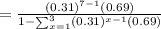
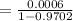
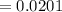
d) - Display that all possibilities actually added up to 100% that is.

`p(x\geq1)=p(x=1)+p(x=2)+p(x=3)...........`

`=q^(1-1)p+q^(2-1)p+q^(3-1)p`

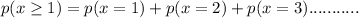
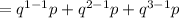
by solving
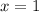`x=1` then, we get

`=(p)/(1-q) =(0.69)/(1-031)`

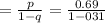
So, we get 1 or 100%.