Answer:

Explanation:
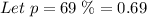
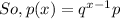
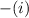
a) - The probability which Jeff requires at exactly three advances that is,
Then, put the value of
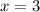 in eq - i
in eq - i
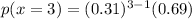

b) - The probability which Jeff requires at least three advances that is,
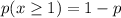
Put the value of
 in the eq
in the eq

c) - Considering that he has only made four advances, the probability would be that he will require at least three more advances that is.
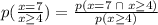
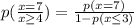
Then, put the value in the eq - i
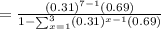
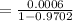
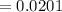
d) - Display that all possibilities actually added up to 100% that is.
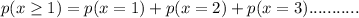
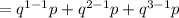
by solving
 then, we get
then, we get
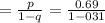
So, we get 1 or 100%.