Question

The taxiways and runways of a major airport are carefully monitored to expedite takeoffs and landings and to prevent collisions. If a pedestrian or vehicle enters a radiocontrolled surface at an airport without receiving permission, this is called a deviation and incursion. Suppose the mean number of deviations and incursions per year at the Los Angeles International Airport (LAX) is 2. Find the probability that exactly 3 serious deviations and incursions will occur at LAX in a randomly selected year

Answer 1

18.04% probability that exactly 3 serious deviations and incursions will occur at LAX in a randomly selected year

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given time interval.

Suppose the mean number of deviations and incursions per year at the Los Angeles International Airport (LAX) is 2.

This means that
`\mu = 2`

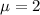
Find the probability that exactly 3 serious deviations and incursions will occur at LAX in a randomly selected year

This is P(X = 3).

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 3) = (e^(-2)*2^(3))/((3)!) = 0.1804`

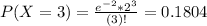
18.04% probability that exactly 3 serious deviations and incursions will occur at LAX in a randomly selected year