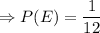Question

A number cube has faces numbered 1 through 6, and a coin has two sides, "heads" and "tails". The

number cube will be rolled once, and the coin will be flipped once. Find the probability that the
number cube shows a 6 or the coin shows "heads." (Express your answers as fractions in lowest
terms.)

Answer 1

The required probability is
`(1)/(12)`.

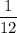Explanation:

Let A be the event of rolling the number cube.

Let B be the event of tossing the coin.

Total number of possibilities of rolling the number cube and tossing the coin are 12 here.

`\{(1,H),(2,H),(3,H),(4,H),(5,H),(6,H),(1,T),(2,T),(3,T),(4,T),(5,T),(6,T)\}`

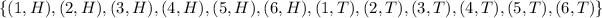
where H means Head on toss of coin and T means Tails on toss of coin.

Formula for probability of an event E is:

`P(E) = \frac{\text{Number of favorable cases}}{\text {Total number of cases}}`

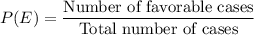
Here, we have to find the probability of event 'E' i.e. getting a 6 on number cube and heads on coin.

Number of favorable cases are 1 and total cases are 12.

`\Rightarrow P(E) = (1)/(12)`