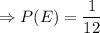Answer:
The required probability is
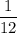 .
.
Explanation:
Let A be the event of rolling the number cube.
Let B be the event of tossing the coin.
Total number of possibilities of rolling the number cube and tossing the coin are 12 here.

where H means Head on toss of coin and T means Tails on toss of coin.
Formula for probability of an event E is:
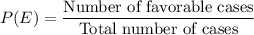
Here, we have to find the probability of event 'E' i.e. getting a 6 on number cube and heads on coin.
Number of favorable cases are 1 and total cases are 12.