Question

You have $4000 to invest. If you'd like to earn exactly $638

in interest each year, how much should you invest in each of
two accounts, one that earns 8% per year and one that
earns 21% per year. (Round your answer to the nearest
dollar)
8%: $
21%: $

Answer 1

8%: $1554

21%: $2446

Explanation:

This is a simple interest problem.

The simple interest formula is given by:

`E = P*I*t`

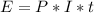
In which E are the earnings, P is the principal(the initial amount of money), I is the interest rate(yearly, as a decimal) and t is the time.

After t years, the total amount of money is:

`T = E + P`.

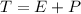In this question:

Two earnings, that i am going to call A(8% per year) and B(21% per year).

Two principals, for A i am going to call P and for B it is the rest, so 4000 - P.

A:

One year, so
`t = 1`

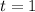
8% interest, so
`r = 0.08`

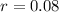
Earnings A.

`A = P*I*t`

`A = 0.08P`

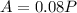
B:

21% interest, so
`r = 0.21`

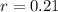
Principal (4000 - P).

`B = P*I*t`

`B = 0.21*(4000 - P)`

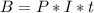
You'd like to earn exactly $638 in interest each year.

This means that
`A + B = 638`

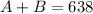
Then

`B = 638 - A`

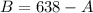
Now we have to solve the following system:

`A = 0.08P`

`638 - A = 0.21*(4000 - P)`

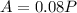
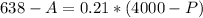
So, on the second equation:

`A = 638 - 0.21*(4000 - P)`

Replacing on the first:

`A = 0.08P`

`638 - 0.21*(4000 - P) = 0.08P`

`638 - 840 + 0.21P = 0.08P`

`0.21P - 0.08P = 840 - 638`

`0.13P = 202`

`P = (202)/(0.13)`

`P = 1553.8`

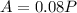
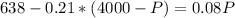
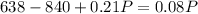
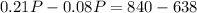
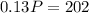
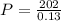
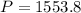
Rounding up to the nearest integer

P = 1554.

So on A, the 8% interest, you invest $1554.

On B, the 21% interest, you invest 4000 - 1554 = $2446.