Answer:
8%: $1554
21%: $2446
Explanation:
This is a simple interest problem.
The simple interest formula is given by:
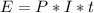
In which E are the earnings, P is the principal(the initial amount of money), I is the interest rate(yearly, as a decimal) and t is the time.
After t years, the total amount of money is:
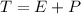 .
.
In this question:
Two earnings, that i am going to call A(8% per year) and B(21% per year).
Two principals, for A i am going to call P and for B it is the rest, so 4000 - P.
A:
One year, so
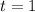
8% interest, so
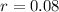
Earnings A.
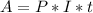
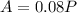
B:
21% interest, so
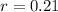
Principal (4000 - P).
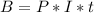
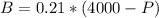
You'd like to earn exactly $638 in interest each year.
This means that
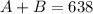
Then
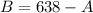
Now we have to solve the following system:
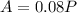
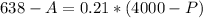
So, on the second equation:
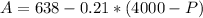
Replacing on the first:
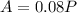
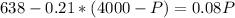
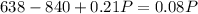
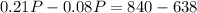
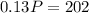
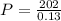
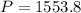
Rounding up to the nearest integer
P = 1554.
So on A, the 8% interest, you invest $1554.
On B, the 21% interest, you invest 4000 - 1554 = $2446.