Question

A pediatrician wants to determine the relation that may exist between a​ child's height and head circumference. She randomly selects 5 children and measures their height and head circumference. The data are summarized below. Find the residuals from the regression and verify that the residuals are approximately normally distributed. Height​ (inches), x 26.75 25.5 26.5 27 25 Head Circumference​ (inches), y 17.3 17.1 17.3 17.5 16.9

Answer 1

`y=0.259 x +10.447`

Now we can find the residulls like this:

`e_1 = 17.3 - 17.375 = -0.075`

`e_2 = 17.1 - 17.052 = 0.049`

`e_3 = 17.3 - 17.311 = -0.011`

`e_4 = 17.5 - 17.440 = 0.06`

`e_5 = 16.9 - 16.922 = -0.022`

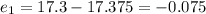
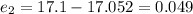
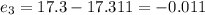
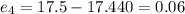
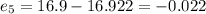
So then we can see that the residuals are not with an specified pattern (alternating sign) so then we can conclude that are distributed normally

Explanation:

We have the following data given:

Height​ (inches), x 26.75 25.5 26.5 27 25

Head Circumference​ (inches), y 17.3 17.1 17.3 17.5 16.9

We need to find a linear model
`y = mx +b`

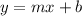
For this case we need to calculate the slope with the following formula:

`m=(S_(xy))/(S_(xx))`

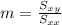
Where:

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)`

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)`

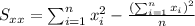
So we can find the sums like this:

`\sum_(i=1)^n x_i =130.75`

`\sum_(i=1)^n y_i =86.1`

`\sum_(i=1)^n x^2_i =3422.06`

`\sum_(i=1)^n y^2_i = 1482.85`

`\sum_(i=1)^n x_i y_i =2252.28`

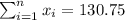
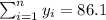
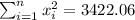
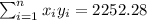
With these we can find the sums:

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)=3422.06-(130.75^2)/(5)=2.95`

`S_(xy)=\sum_(i=1)^n x_i y_i -\frac{(\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i)}=2252.28-(130.75*86.1)/(5)=0.765`

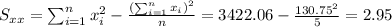
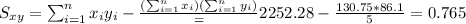
And the slope would be:

`m=(0.765)/(2.95)=0.259`

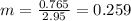
Nowe we can find the means for x and y like this:

`\bar x= (\sum x_i)/(n)=(130.75)/(5)=26.15`

`\bar y= (\sum y_i)/(n)=(86.1)/(5)=17.22`

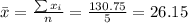
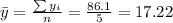
And we can find the intercept using this:

`b=\bar y -m \bar x=17.22-(0.259*26.15)=10.447`

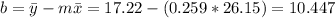
So the line would be given by:

`y=0.259 x +10.447`

Now we can find the residulls like this:

`e_1 = 17.3 - 17.375 = -0.075`

`e_2 = 17.1 - 17.052 = 0.049`

`e_3 = 17.3 - 17.311 = -0.011`

`e_4 = 17.5 - 17.440 = 0.06`

`e_5 = 16.9 - 16.922 = -0.022`

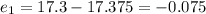
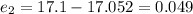
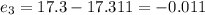
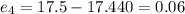
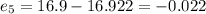
So then we can see that the residuals are not with an specified pattern (alternating sign) so then we can conclude that are distributed normally