We have been given that in ΔJKL, k = 22 cm, ∠L=23° and ∠J=26°. We are asked to find the length of j to the nearest tenth of a centimeter.
We will use law of sines to solve for side j.
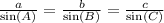 , where, a, b and c are opposite sides to angles A, B and C respectively.
, where, a, b and c are opposite sides to angles A, B and C respectively.
We need to find measure of angle K to apply law of sine to our given problem.
Using angle sum property, we will get:
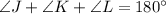
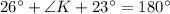
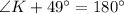
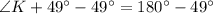
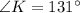


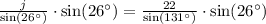
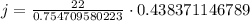

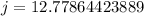
Upon rounding to nearest tenth, we will get:
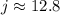
Therefore, the length of j is approximately 12.8 cm.