Answer:
Check the explanation
Explanation:
Let X denotes steel ball and Y denotes diamond
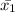 = 1/9( 50+57+......+51+53)
= 1/9( 50+57+......+51+53)
=530/9
=58.89
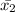 = 1/9( 52+ 56+....+ 51+ 56)
= 1/9( 52+ 56+....+ 51+ 56)
=543/9
=60.33
difference = d =(60.33- 58.89)
=1.44
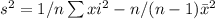
s12 = 1/9( 502+572+......+512+532) -9/8 (58.89)2
=31686/8 - 9/8( 3468.03)
=3960.75 - 3901.53
=59.22
s1 = 7.69
s22 = 1/9( 522+ 562+....+ 512+ 562) -9/8 (60.33)2
=33295/8 - 9/8 (3640.11)
=4161.875 - 4095.12
=66.75
s2 =8.17
sample standard deviation for difference is
s=
![√([(n1-1)s_1^2+ (n2-1)s_2^2]/(n1+n2-2))](https://img.qammunity.org/2021/formulas/mathematics/college/t1haxnyawmtpj5qs2x8a8wof4nwvsk6cpl.png)
=
![√([(9-1)*59.22+ (9-1)*66.75]/(9+9-2))](https://img.qammunity.org/2021/formulas/mathematics/college/2j1pgbn90u4q9o4db7truq8evkcx1cegbn.png)
=
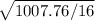
=7.93
sd =
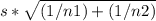
=
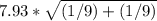
=7.93* 0.47
=3.74
For 95% confidence level
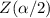 =1.96
=1.96
confidence interval is

=(1.44 - 1.96* 3.75 , 1.44+1.96* 3.75)
=(1.44 - 7.35 , 1.44 + 7.35)
=(-2.31, 8.79)
There is sufficient evidence to conclude that the two indenters produce different hardness readings.