Answer:
Null hypothesis:
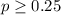
Alternative hypothesis:
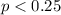
The statistic would be given by:
 (1)
(1)
Now we need to find the critical value for the rejection zone of the null hypothesis. Since we have a left tailed test we need to find in the normal standard distirbution a value who accumulate 0.05 of the area in the left tail and we got:
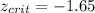
And the best choice for this case would be:
z < − 1.65
Explanation:
Information provided
n=2431 represent the random sample taken
 estimated proportion of interest
estimated proportion of interest
 is the value that we want to test
is the value that we want to test
 represent the significance level
represent the significance level
Confidence=95% or 0.95
z would represent the statistic
Hypothesis to test
We want to verify if the true proportion of Americans who reduced meat consumption last year is less than 0.25, then the system of hypothesis are :
Null hypothesis:
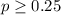
Alternative hypothesis:
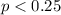
The statistic would be given by:
 (1)
(1)
Now we need to find the critical value for the rejection zone of the null hypothesis. Since we have a left tailed test we need to find in the normal standard distirbution a value who accumulate 0.05 of the area in the left tail and we got:
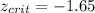
And the best choice for this case would be:
z < − 1.65