Answer:
The 95% confidence interval for the proportion of parents that are satisfied with their children's education is (0.4118, 0.4618). 0.5 is not part of the confidence interval, so this represents evidence that parents' attitudes toward the quality of education have changed.
Explanation:
We have to see if 50% = 0.5 is part of the confidence interval.
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of
 .
.
For this problem, we have that:
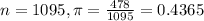
95% confidence level
So
 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
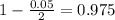 , so
, so
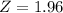 .
.
The lower limit of this interval is:
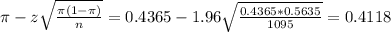
The upper limit of this interval is:
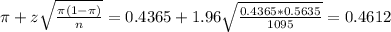
The 95% confidence interval for the proportion of parents that are satisfied with their children's education is (0.4118, 0.4618). 0.5 is not part of the confidence interval, so this represents evidence that parents' attitudes toward the quality of education have changed.