Question

Suppose an archaeologist discovers seven fossil skeletons from a previously unknown species of miniature horse. Reconstructions of the skeletons of these seven miniature horses show the shoulder heights (in centimeters) to be 45.3 47.1 44.2 46.8 46.5 45.5 47.6 For these sample data, the mean is x¯ = 46.14 and the sample standard deviation is s = 1.19. Let µ be the mean shoulder height (in centimeters) for this entire species of miniature horse, and assume that the population of shoulder heights is approximately normal. (a) Construct a 99% confidence interval for µ, the mean shoulder height of the entire population of such horses. (b) Someone claims that the mean shoulder heights of these horses is about 48 cm or higher. Based on the confidence interval, is it reasonable to believe this? (c) If the sample size were n = 10, would the confidence interval be narrower or wider?

Answer 1

a)
`46.14-3.707(1.19)/(√(7))=44.47`

`46.14+3.707(1.19)/(√(7))=47.81`

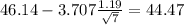
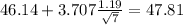
b) For this case the upper limit for the confidence interval is lower than 48 so then at 1% of significance we can't conclude that the claim given is true.

c)
`ME = t_(\alpha/2)(s)/(√(n))`

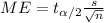
If we reduce the sample size from 30 to 10 we will have an interval wider since the margin of error would be larger

Explanation:

Data given

`\bar X=46.14` represent the sample mean

`\mu` population mean

s=1.19 represent the sample standard deviation

n=7 represent the sample size

Part a

The confidence interval for the mean is given by the following formula:

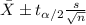`\bar X \pm t_(\alpha/2)(s)/(√(n))` (1)

The degrees of freedom are given by:

`df=n-1=7-1=6`

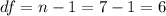
The Confidence level is 0.99 or 99%, the significance would be
`\alpha=0.01` and
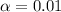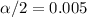`\alpha/2 =0.005`, and the critical value for this case is
`t_(\alpha/2)=3.707`

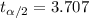
Replacing we got:

`46.14-3.707(1.19)/(√(7))=44.47`

`46.14+3.707(1.19)/(√(7))=47.81`

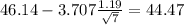
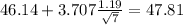
Part b

For this case the upper limit for the confidence interval is lower than 48 so then at 1% of significance we can't conclude that the claim given is true.

Part c

For this case we need to take in count that the margin of error is given by:

`ME = t_(\alpha/2)(s)/(√(n))`

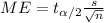
If we reduce the sample size from 30 to 10 we will have an interval wider since the margin of error would be larger