Question

When it is operating properly, a chemical plant has a daily production rate that is normally distributed with a mean of 885 tons/day and a standard deviation of 42 tons/day. During an analysis of period, the output is measured with random sampling on 60 consecutive days, and the mean output is found to be x=875 tons/day. The manager claims that at least 95 % probability that the plant is operating properly. Is he right? Justify your answer!

Answer 1

The test statistic Z = 1.844 < 1.96 at 0.05 level of significance

Null hypothesis is accepted

Yes he is right

The manager claims that at least 95 % probability that the plant is operating properly

Explanation:

Explanation:-

Given data Population mean

μ = 885 tons /day

Given random sample size

n = 60

mean of the sample

x⁻ = 875 tons/day

The standard deviation of the Population

σ = 42 tons/day

Null hypothesis:- H₀: The manager claims that at least 95 % probability that the plant is operating properly

Alternative Hypothesis :H₁: The manager do not claims that at least 95 % probability that the plant is operating properly

Level of significance = 0.05

The test statistic

`Z = (x^(-) -mean)/((S.D)/(√(n) ) )`

`Z = (875 -885)/((42)/(√(60) ) )`

`Z = (-10)/(5.422) = -1.844`

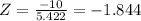
|Z| = |-1.844| = 1.844

The tabulated value

`Z_{(0.05)/(2) } = Z_(0.025) = 1.96`

The calculated value Z = 1.844 < 1.96 at 0.05 level of significance

Null hypothesis is accepted

Conclusion:-

The manager claims that at least 95 % probability that the plant is operating properly