Question

The FBI wants to determine the effectiveness of their 10 Most Wanted list. To do so, they need to find out the fraction of people who appear on the list that are actually caught. Step 2 of 2 : Suppose a sample of 517 suspected criminals is drawn. Of these people, 211 were captured. Using the data, construct the 98% confidence interval for the population proportion of people who are captured after appearing on the 10 Most Wanted list. Round your answers to three decimal places.

Answer 1

98% of confidence intervals for the Population proportion of people who captured after appearing on the 10 most wanted list

(0.3583 , 0.4579)

Explanation:

Explanation:-

Given sample size 'n' = 517

Given data Suppose a sample of 517 suspected criminals is drawn. Of these people, 211 were captured.

'x' =211

The sample proportion

`p^(-) = (x)/(n) = (211)/(517) =0.4081`

`q^(-) = 1-p^(-) = 1- 0.4081 = 0.5919`

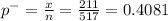
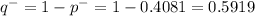
98% of confidence intervals for the Population proportion of people who captured after appearing on the 10 most wanted list

`(p^(-) - Z_{(\alpha )/(2) } \sqrt{(p^(-) (1-p^(-) ))/(n) } , p^(-) + Z_{(\alpha )/(2) } \sqrt{(p^(-) (1-p^(-) )/(n) } )`

`(0.4081 - 2.326 \sqrt{(0.4081 (0.5919 ))/(517) } , 0.4081+ 2.326\sqrt{(0.4081(0.5919 )/(517) } )`

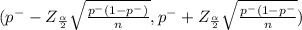
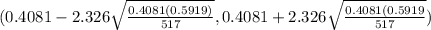
(0.4081-0.0498 , 0.4081 +0.0498)

(0.3583 , 0.4579)

Conclusion:-

98% of confidence intervals for the Population proportion of people who captured after appearing on the 10 most wanted list

(0.3583 , 0.4579)