Question

It was claimed that when tossing a fair coin 4 times it is quite likely to not obtain 2 heads and 2 tails. However, when tossing a fair coin 4,000 times one should expect to obtain number of tails in the range between 1940 and 2060. Let us compare the situation for 2 versus 2,000 coins. Let X be the number of heads when tossing a fair coin 2 times and let Y be the number of heads when tossing a fair coin 2,000 times.

1. P(940 ≤ Y ≤ 1,060) is equal to:______.2. E(X) is equal to:______.3. The standard deviation of X is equal to:______.4. E(Y) is equal to:_______.

Answer 1

1. P(940 ≤ Y ≤ 1,060) is equal to: 0.9927.

2. E(X) is equal to: 1.

3. The standard deviation of X is equal to: 0.707.

4. E(Y) is equal to: 1,000.

Explanation:

The number of heads (or tails) in a repeated toss of a coin can be modeled as a binomial random variable.

When the number of trials becomes bigger, the calculations for the binomial distribution became more tedious, as we have to calculate it for each individual number of tails or head.

This can be solved with the approximation to the normal distribution, where we treat the variable as continuous and the calculations are easier.

For n=2, the calculations for the binomial distribution are feasible and accurate.

The expected value for the number of heads is:

`E(X)=n\cdot p=2\cdot0.5=1`

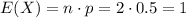
where n is the number of trials and p the probability of heads.

The standard deviation can be calculated as:

`\sigma_x=√(np(1-p))=√(2\cdot0.5\cdot0.5)=√(0.5)\approx0.707`

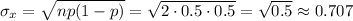
For n=2000 trials, the normal approximation is reasonable.

The mean of the normal distribution can be calculated as:

`E(Y)=\mu=n\cdot p=2,000\cdot 0.5=1,000`

where n is the number of trials and p the probability of heads.

The standard deviation of the normal approximation can be calculated as:

`\sigma_y=√(np(1-p))=√(2,000\cdot0.5\cdot0.5)=√(500)\approx22.36`

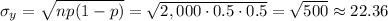
To calculate then the probability P(940 ≤ Y ≤ 1,060), we calculate the z-score for each value:

`z_1=(Y_1-\mu)/(\sigma)=(940-1000)/(22.36)=(-60)/(22.36)=-2.683\\\\\\z_2=(Y_2-\mu)/(\sigma)=(1060-1000)/(22.36)=(60)/(22.36)=2.683`

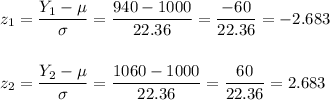
Now, we can calculate the probability as:

`P(940\leqY\leq1060)=P(-2.683<z<2.683)=P(|z|<2.683)=0.9927`