Taylor's function is exponential with a decay rate of 6.8%.
In Mathematics and Statistics, a population or material that decreases at a specific period of time represents an exponential decay.
This ultimately implies that, a mathematical model for any population or material that decreases by r percent per unit of time is an exponential function of this form:
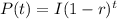
Where:
- P(t) represents the final population or volume.
- t represents the time or number of years or days.
- I represents the initial population or volume.
- r represents the decay rate.
Since Taylor's function models the volume of a material that decreases by 6.8% each year, it ultimately implies that Taylor's function is an exponential function with a decay rate of 6.8%.
Complete Question;
Taylor used the function f(x) to model the change in the volume of a synthetic material. The volume of the material decreases by 6.8% each year. Select a statement from each of the dropdown menus below to accurately complete the sentence describing Taylor's function.
Taylor's function is ____ with ____ 6.8%.