Question

Taylor used the function f(x) to model the change in the volume of a synthetic material. The volume of the material decreases by 6.8% each year. Select a statement from each of the dropdown menus below to accurately complete the sentence describing Taylor's function. Taylor's function is with 6.8%.

Answer 1

Answer: exponential with a decay rate of

Explanation:

Answer 2

Taylor's function is exponential with a decay rate of 6.8%.

In Mathematics and Statistics, a population or material that decreases at a specific period of time represents an exponential decay.

This ultimately implies that, a mathematical model for any population or material that decreases by r percent per unit of time is an exponential function of this form:

`P(t) = I(1 - r)^t`

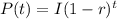
Where:

• P(t) represents the final population or volume.
• t represents the time or number of years or days.
• I represents the initial population or volume.
• r represents the decay rate.

Since Taylor's function models the volume of a material that decreases by 6.8% each year, it ultimately implies that Taylor's function is an exponential function with a decay rate of 6.8%.

Complete Question;

Taylor used the function f(x) to model the change in the volume of a synthetic material. The volume of the material decreases by 6.8% each year. Select a statement from each of the dropdown menus below to accurately complete the sentence describing Taylor's function.

Taylor's function is ____ with ____ 6.8%.