Question

A child throws a ball upward with an initial velocity of 15 ft/s from a height of 2 feet. Let ℎ = 0 and solve. If no one catches the ball, how long will it be in the air? Round to the nearest hundredth. ℎ = −16 2 + v + where v is the initial upward velocity with starting height

Answer 1

1.056 seconds

Explanation:

Solution:-

- When a ball is thrown vertically in air from a height of "so" from the ground at a velocity of " vo " it follows a parabolic trajectory. The ball undergoes its upward motion against gravity. Hence, it has negative acceleration of a = -g = -32 ft/s^2.

- When the balls reaches its maximum height in air, it starts its downward journey under the complete influence of gravity; hence, it accelerates with a = +g = 32 ft/s^2.

- The entire trajectory of the ball is governed by the constant acceleration "a" due to gravity and neglecting any other effects on the ball i.e air resistance.

- There are three kinematic equation of motion valid for any particle undergoing independent one dimensional motion with constant acceleration.

- For vertical trajectory the displacement "h" from the ground is given by the second kinematic equation of motion:

h - so = vo*t + 0.5*a*t^2

h = vo*t + 0.5*a*t^2 + so

Where the parameters are given as:

so = 2 feet

vo = 15 ft/s

a = - 32 ft/s^2

Therefore we have:

h = 15*t + 0.5*(-32)*t^2 + 2

h = -16t^2 + 15t + 2

- To determine the amount of time the ball is in air the displacement is given by the distance from the ground. The journey starts when the ball is thrown from height "so" and ends when it strikes the ground; hence, at h = 0 ft.

0 = -16t^2 + 15t + 2

0 = 16t^2 -15t - 2

- Use the quadratic formula to solve for time "t":

`t = (-b+/-√(b^2 - 4*a*c) )/(2a) \\\\at^2 + bt + c = 0`

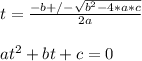
- Plug in the respective constants:

`t = (15+/-√(15^2 - 4*16*-2) )/(32) \\\\ t = (15+/-18.78829 )/(32) \\\\t = 1.056 s`

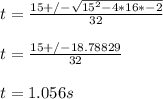
- The total time for ball in air would be 1.056 seconds. ( Neglect the negative value of time )