Answer:
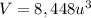
Explanation:
The volume of a prism is given by:
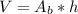
where
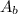 is the area of the base, and
is the area of the base, and
 is the height of thr prism.
is the height of thr prism.
We know that the height is:
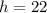 u
u
and the bases of this prism are hexagons.
Thus the area of the base is the area of a regular hexagon:
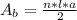
where
 is the number of sides: for an hexagon:
is the number of sides: for an hexagon:
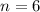
 is the length of each side:
is the length of each side:
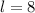 u,
u,
and
 is the apothem:
is the apothem:
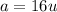
we substitute all of this to find the area of the base:
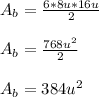
and finally we use the formula for the volume:
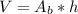
we get the following:

which is the third option