Sphere A and Sphere B , are similar. The volumes of A and B, are 17 and 136 cubic centimetres, respectively. The diameter of B , is 6 centimetres. Determine the corresponding di…

Question

asked May 23, 2021 229k views

1 Answer

Stan Sokolov · Answer 1 · 2021-05-29T12:31:55+0000

Answer:

3

Explanation:

Given: Sphere A and Sphere B are similar.

The volumes of A and B are 17
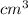cm^3 and 136

The diameter of B is 6 cm.

To find: diameter of A

Solution:

Let R denotes radius of sphere A and r denotes radius of sphere B.

Radius of sphere A= R

Diameter of sphere B = 6 cm

So, radius of sphere B (r) =
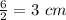
$(6)/(2)=3\,\,cm$

Volume of sphere is
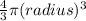
$(4)/(3)\pi(radius)^3$

Volume of sphere A =
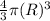
$(4)/(3)\pi(R)^3$

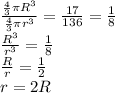
$((4)/(3)\pi R^3)/((4)/(3)\pi r^3)=(17)/(136)=(1)/(8)\\(R^3)/(r^3)=(1)/(8)\\(R)/(r)=(1)/(2)\\r=2R$

Put r = 3 cm

$3=2R\\R=(3)/(2)=1.5\,\,cm$

Diameter of sphere A = 2 × Diameter

= 2 × 1.5

=3 cm