Answer:
1)
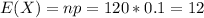
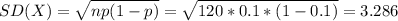
For this case we can interpret that the expected variation around the mean is about 3.3 people approximated
2)

And we can use the normal approximation given by:
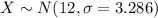
And we can use the z score formula given by:
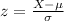
And if we find the z score for 16 we got:
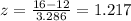
And we can find this probability using the normal standard distribution or excel and we got:
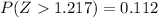
3) For this case we can conclude that the probability to find 16 or more individuals left handed in a sample of 120 is about 0.112 or 11.2%
Step-by-step explanation:
Let X represent the random variable for the number of residents who are left handed
And for this case we can model this variable with this distirbution:
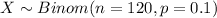
Part 1
The mean is given by:
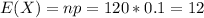
And the deviation would be:
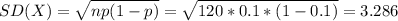
For this case we can interpret that the expected variation around the mean is about 3.3 people approximated
Part 2
We want to calculate this probability:

And we can use the normal approximation given by:
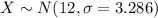
And we can use the z score formula given by:
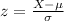
And if we find the z score for 16 we got:
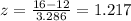
And we can find this probability using the normal standard distribution or excel and we got:
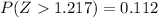
Part 3
For this case we can conclude that the probability to find 16 or more individuals left handed in a sample of 120 is about 0.112 or 11.2%