Question

About 10% of people in the United States are left handed. Suppose we take a sample of 120 U.S. Residents, and let X = the number of residents who are left handed. 1. Calculate the mean and standard deviation of the sampling distribution of X. Interpret the standard deviation. 2. Calculate the probability that 16 or more individuals in the sample are left handed. Show your work. 3. Interpret your answer from #2.

Answer 1

The mean and standard deviation of the sampling distribution of X can be calculated using the population proportion and sample size. The probability that 16 or more individuals in the sample are left-handed can be calculated using the binomial distribution. The standard deviation of the sampling distribution represents the average amount of variability or spread of the sample means around the population mean.

Step-by-step explanation:

The question asks about the sampling distribution of X, where X represents the number of residents who are left-handed in a sample of 120 U.S. residents. To calculate the mean and standard deviation of the sampling distribution of X, we need to know the mean and standard deviation of the population. The mean of the sampling distribution of X is equal to the population proportion, which is 0.10 (10%). The standard deviation of the sampling distribution of X can be calculated using the formula sqrt(p(1-p)/n), where p is the population proportion and n is the sample size. Plugging in the values, we get sqrt(0.10(1-0.10)/120) ≈ 0.0287.

To calculate the probability that 16 or more individuals in the sample are left-handed, we need to use the binomial distribution. The formula for the probability of X successes in a binomial distribution is P(X=k) = (n choose k)(p^k)(1-p)^(n-k), where n is the sample size, k is the number of successes, and p is the probability of success. In this case, n=120, k=16, and p=0.10. Plugging in the values, we can calculate the probability that 16 or more individuals in the sample are left-handed.

The interpretation of the standard deviation of the sampling distribution is that it represents the average amount of variability or spread of the sample means around the population mean. In other words, it measures how much the sample means are likely to differ from the population mean. In this case, a standard deviation of 0.0287 means that the sample means of the number of left-handed residents are likely to vary by about 0.0287 from the population proportion of 0.10.

Answer 2

1)
`E(X) = np = 120*0.1 =12`

`SD(X) = √(np(1-p))= √(120*0.1*(1-0.1)) =3.286`

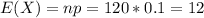
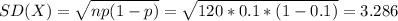
For this case we can interpret that the expected variation around the mean is about 3.3 people approximated

2)
`P(X\geq 16)`

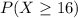
And we can use the normal approximation given by:

`X \sim N(12, \sigma =3.286)`

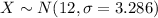
And we can use the z score formula given by:

`z = (X -\mu)/(\sigma)`

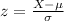
And if we find the z score for 16 we got:

`z = (16-12)/(3.286)= 1.217`

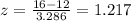
And we can find this probability using the normal standard distribution or excel and we got:

`P(Z>1.217) = 0.112`

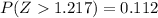
3) For this case we can conclude that the probability to find 16 or more individuals left handed in a sample of 120 is about 0.112 or 11.2%

Step-by-step explanation:

Let X represent the random variable for the number of residents who are left handed

And for this case we can model this variable with this distirbution:

`X\sim Binom(n= 120 , p =0.1)`

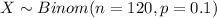
Part 1

The mean is given by:

`E(X) = np = 120*0.1 =12`

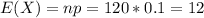
And the deviation would be:

`SD(X) = √(np(1-p))= √(120*0.1*(1-0.1)) =3.286`

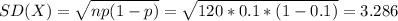
For this case we can interpret that the expected variation around the mean is about 3.3 people approximated

Part 2

We want to calculate this probability:

`P(X\geq 16)`

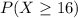
And we can use the normal approximation given by:

`X \sim N(12, \sigma =3.286)`

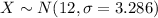
And we can use the z score formula given by:

`z = (X -\mu)/(\sigma)`

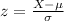
And if we find the z score for 16 we got:

`z = (16-12)/(3.286)= 1.217`

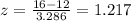
And we can find this probability using the normal standard distribution or excel and we got:

`P(Z>1.217) = 0.112`

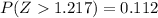
Part 3

For this case we can conclude that the probability to find 16 or more individuals left handed in a sample of 120 is about 0.112 or 11.2%