Question

Solve the following problem:

Given: △SAL, SA = LA

AT − ∠bisector

Prove: m∠L = m∠S

Answer 1

Explanation:

First, we know that △ALT ≅ △AST, because of Side Angle Side Theorem. Next, we know that AL ≅ AS, because it's given.

Since A = A, we can remove A and it gives us m∠L = m∠S.

If you need to show work in math terms, your answer should look something like this:

1. △ ALT ≅ △AST - SAS

2. AL ≅ AS - Given

3. m∠ L ≅ m∠S

Hope this helped!

Answer 2

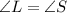`\angle L=\angle S` using congruence rule

Explanation:

Given: ΔSAL, SA = LA and AT is the bisector of
`\angle A`

To prove:
`\angle L=\angle S`

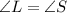
Proof:

Two triangles are congruent if they have same shape and same size.

Consider triangles ALT and AST

AL = AS

As AT bisects
`\angle A`,
`\angle LAT=\angle SAT\\`

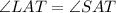
AT = AT (common side)

So,
`\Delta ALT\cong \Delta AST` ( by SAS congruence rule )

Here, SAS denotes side-angle-side

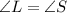`\angle L=\angle S` (using corresponding parts of congruent triangles)

Hence proved