Question

If 4% of 1,000 babies in an African population are born with a severe form of sickle-cell anemia (ss), how many babies will be more resistant to malaria because they are heterozygous (Ss) for the sickle-cell gene?

Answer 1

Total
`320` babies are heterozygous (Ss) for the sickle-cell gene

Step-by-step explanation:

It is given that babies with sickle cell anemia disease have genotype "ss"

The number of babies with sickle cell anemia disease

`= (4)/(100) * 1000\\= 40`

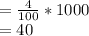
Out of
`1000`, nearly
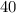`40` species have ss genotype

Let us take "s" be recessive to "S"

Also let us assume that the given population is in Hardy Weinberg's equation-

Then frequency of recessive genotype would be
`0.04`

`q^2 = 0.04\\`

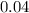
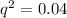
Frequency of recessive "s" allele will be

`q = 0.2`

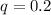
As per Hardy Weinberg's first equilibrium equation, we have -

`p + q = 1\\`

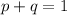
Substituting the values of "q" in above equation, we get -

`p = 1-0.2\\p = 0.8`

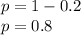
Frequency of dominant genotype would be

`p^2 = 0.8^2\\p^2 = 0.64`

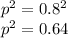
Hardy Weinberg's second equilibrium equation is

`p^2 + q^2 +2pq = 1\\`

Substituting the available values in above equation we get -

`2pq = 1 - 0.04 -0.64\\2pq = 0.32`

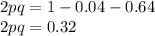
Hence,
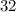`32` % of
`1000` babies are heterozygous (Ss) for the sickle-cell gene

Thus, total
`320` babies are heterozygous (Ss) for the sickle-cell gene