Answer:
Total
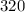 babies are heterozygous (Ss) for the sickle-cell gene
babies are heterozygous (Ss) for the sickle-cell gene
Step-by-step explanation:
It is given that babies with sickle cell anemia disease have genotype "ss"
The number of babies with sickle cell anemia disease
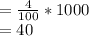
Out of
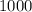 , nearly
, nearly
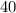 species have ss genotype
species have ss genotype
Let us take "s" be recessive to "S"
Also let us assume that the given population is in Hardy Weinberg's equation-
Then frequency of recessive genotype would be
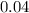
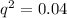
Frequency of recessive "s" allele will be
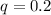
As per Hardy Weinberg's first equilibrium equation, we have -
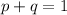
Substituting the values of "q" in above equation, we get -
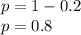
Frequency of dominant genotype would be
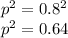
Hardy Weinberg's second equilibrium equation is
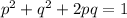
Substituting the available values in above equation we get -
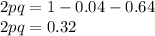
Hence,
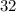 % of
% of
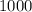 babies are heterozygous (Ss) for the sickle-cell gene
babies are heterozygous (Ss) for the sickle-cell gene
Thus, total
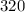 babies are heterozygous (Ss) for the sickle-cell gene
babies are heterozygous (Ss) for the sickle-cell gene