Total surface area of Cuboid:
If
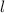 be the length of cuboid,
be the length of cuboid,
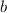 be the breadth of cuboid and
be the breadth of cuboid and
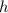 be the height of cuboid, then its total surface area (TSA) of cuboid is given by,
be the height of cuboid, then its total surface area (TSA) of cuboid is given by,
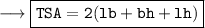
A cuboid is also known as rectangular prism.
Elucidation:
We need to find the surface area of the cuboid or rectangular prism whose length, breadth and height are given.
- Length = 6 1/2 = 6.5cm
- Breadth = 2 1/2 = 2.5cm
- Height = 2 2/2 = 2.5cm
Now by using the formula of surface area nd substituting the given values, we get the following results:
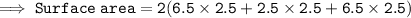
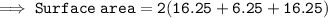
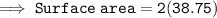

Hence, this is our required solution for this question.

Additional information:
- Volume of cylinder = πr²h
- T.S.A of cylinder = 2πrh + 2πr²
- Volume of cone = ⅓ πr²h
- C.S.A of cone = πrl
- T.S.A of cone = πrl + πr²
- Volume of cuboid = l * b * h
- C.S.A of cuboid = 2(l + b)h
- T.S.A of cuboid = 2(lb + bh + lh)
- C.S.A of cube = 4a²
- T.S.A of cube = 6a²
- Volume of cube = a³
- Volume of sphere = 4/3πr³
- Surface area of sphere = 4πr²
- Volume of hemisphere = ⅔ πr³
- C.S.A of hemisphere = 2πr²
- T.S.A of hemisphere = 3πr²