Another triple integral. We're integrating over the interior of the sphere
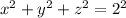
Let's do the outer integral over z. z stays within the sphere so it goes from -2 to 2.
For the middle integral we have
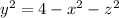
x is the inner integral so at this point we conservatively say its zero. That means y goes from
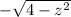 and
and
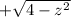
Similarly the inner integral x goes between

So we rewrite the integral
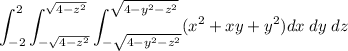
Let's work on the inner one,

There's no z in the integrand, so we treat it as a constant.
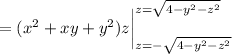
So the middle integral is

I gotta go so I'll stop here, sorry.