Question

Hi guys, can anyone help me with this triple integral? Many thanks:)

Answer 1

Another triple integral. We're integrating over the interior of the sphere

`x^2+y^2+z^2=2^2`

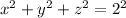
Let's do the outer integral over z. z stays within the sphere so it goes from -2 to 2.

For the middle integral we have

`y^2=4-x^2-z^2`

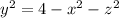
x is the inner integral so at this point we conservatively say its zero. That means y goes from
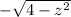`-√(4-z^2)` and
`+√(4-z^2)`

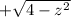
Similarly the inner integral x goes between
`\pm-√(4-y^2-z^2)`

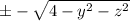
So we rewrite the integral

`\displaystyle \int_(-2)^(2) \int_(-√(4-z^2))^(√(4-z^2)) \int_(-√(4-y^2-z^2))^(√(4-y^2-z^2)) (x^2+xy+y^2)dx \; dy \; dz`

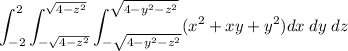
Let's work on the inner one,

`\displaystyle\int_(-√(4-y^2-z^2))^(√(4-y^2-z^2)) (x^2+xy+y^2)dz`

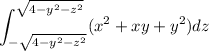
There's no z in the integrand, so we treat it as a constant.

`=(x^2+xy+y^2)z \bigg|_(z=-√(4-y^2-z^2))^(z=√(4-y^2-z^2))`

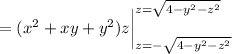
So the middle integral is

`\displaystyle\int_(-√(4-z^2))^(√(4-z^2))2(x^2+xy+y^2)√(4-y^2-z^2) \ dy`

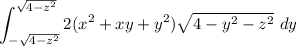
I gotta go so I'll stop here, sorry.

Answer 2

Converting to spherical coordinates makes the task easier:

`\begin{cases}x=\rho\cos\theta\sin\varphi\\y=\rho\sin\theta\sin\varphi\\z=\rho\cos\varphi\end{cases}\implies\mathrm dx\,\mathrm dy\,\mathrm dz=\rho^2\sin\varphi\,\mathrm d\rho\,\mathrm d\theta\,\mathrm d\varphi`

Under this transformation, the integrand reduces to

`x^2+xy+y^2=(1+\cos\theta\sin\theta)\rho^2\sin^2\varphi`

and the integral is

`\displaystyle\iiint_Kx^2+xy+y^2\,\mathrm dx\,\mathrm dy\,\mathrm dz=\int_0^\pi\int_0^(2\pi)\int_0^2(1+\cos\theta\sin\theta)\rho^4\sin^3\varphi\,\mathrm d\rho\,\mathrm d\theta\,\mathrm d\varphi`

You can separate the variables easily in this case, so you can consider the integrals with respect to the individual variables:

`\displaystyle\int_0^\pi\sin^3\varphi\,\mathrm d\varphi=\frac43`

`\displaystyle\int_0^(2\pi)1+\cos\theta\sin\theta\,\mathrm d\theta=2\pi`

`\displaystyle\int_0^2\rho^4\,\mathrm d\rho=\frac{32}5`

Then the triple integral has a value equal to the product of these three integrals, so

`\displaystyle\iiint_Kx^2+xy+y^2\,\mathrm dx\,\mathrm dy\,\mathrm dz=\boxed{(256\pi)/(15)}`