Question

Determine between which consecutive integers the real zeros of f(x) = 2x2 - 5x+1 are located

a between 0&1 and 1&2
c. between 0&1 and 2&3
b. between -1&0 and 2&3
d between 1&2 and 2&3

Answer 1

c edge2020

Explanation:

Answer 2

Answer: c. between 0&1 and 2&3

Explanation:

We want to find the roots of :

y = 2x^2 5x + 1

we can use the Bhaskara equation and find that:

`x = (5 +-√(5^2 - 4*2*1) )/(2*2) = (5 +-√(18) )/(4)`

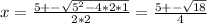
and 4*4 = 16

5*5 = 25

then √18 is a number between 4 and 5.

So the roots are:

x = (5 +√18 )/4 = is a number larger than 2 but smaller than 3 (it can not be bigger than 3 because we know that √18 is smaller than 5, suppose it is equal to 5, then (5 + 5)/4 = 10/4, that is smaller than 3)

2 < (5 +√18 )/4 < 10/4 < 3

x = (5 - √18)/4 = is a number smaller than 1 and bigger than zero (because √18 is smaller than 5 so the number in the parentheses never can be 0, and √18 is bigger than 4, if we take this value we have that:

(5 - 4)/4 = 1/4 = 0.25

then we have: 0 < (5 - √18)/4 < 1/4 < 1

So one root is between 0 and 1, and the other root is between 2 and 3.