In ΔHIJ, the measure of ∠J=90°, the measure of ∠H=84°, and HI = 69 feet. Find the length of IJ to the nearest tenth of a foot.

Question

asked Oct 20, 2021 121k views

2 Answers

Equiman · Answer 1 · 2021-10-26T16:33:03+0000

Answer:

The length of IJ is 68.7 feet.

Explanation:

According to trigonometric identities for a right angled triangle, the sin of an angle is:

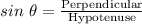
$sin\ \theta=\frac{\text{Perpendicular}}{\text{Hypotenuse}}$

From the provided data we can interpret that:

Perpendicular = x feet

Hypotenuse = 69 feet

θ = 84°

Compute the value of x as follows:

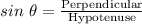
$sin\ \theta=\frac{\text{Perpendicular}}{\text{Hypotenuse}}$

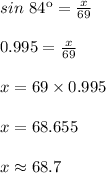
$sin\ 84^{\text{o}}=(x)/(69)\\\\0.995=(x)/(69)\\\\x=69*0.995\\\\x=68.655\\\\x\approx 68.7$

Thus, the length of IJ is 68.7 feet.